컴퓨터에서의 데이터 표현
진법과 진법 변환
정수 표현
실수 표현
디지털 코드
에러 검출 코드
- 진법과 진법 변환
디지털 정보의 단위
1nibble=4bit
1byte=8bit
1byte=1문자(character)영어는 1byte로 1문자, 한글은 2byte가 필요
1word: 특정 CPU에서 취급하는 명령어나 데이터의 길이에 해당하는 비트 수: 8, 16, 32, 64비트 등 8의 배수 가능
MSB(Most Significant Bit): 최상위 비트
LSB(Least Significant BIt) : 최하위 비트
진법
2진법(binary): 0과1 두가지 기호로 표현하는 수의 체계
8진법(octal), 10진법(decima), 16진법(hexadecimal) 등을 주로 사용
8진법은 2진수 3비트, 16진법은 2진수 4비트를 한자리수로 표현가능
16진수는 0-F까지 사용
진법 변환등은 알것이라고 생각하고 생략 하겠음
분수(실수)의 변환
실수는 10진수와 동일하게 진행
소수점은 2를 곱해가면서 2진수로 표현
ex) 45.75
45(10)->101101(2)
0.75(10)->0.11(2)
방법은 0.75*2=1.5처럼 앞자리 1을 계속 소수점 이진수로 빼준다.
그냥 수학적으로 2^-1처럼 생각해서 계산하자!
소수점은 정확하게 표시하지 못하는 경우가 많음(실수는 무한하기 때문에 비트로 표현 불가능)
보수(Complement)
- 최대값(해당 bit에서 가장 큰 표현형)을 형성하는데 서로 보완 관계에 있는 두 수 사이의 관계를 one’s COMPLEMENT라고 한다.
- MODULUS(최대 표현 자리 수)를 형성하는데 서로 보완관계에 있는 두 수 사이의 관계를 two’s COMPLEMENT라고 한다.
ex) 10진수(최대값9)에서의 보수
1진 보수(ONE’S COMPLEMENT): A+B=9, A+B=99...
2진 보수(TWO’S COMPLEMENT): A+B=10, A+B=100…
ex) 2진 보수
1진 보수(ONE’S COMPLEMENT): A+B=1, A+B=11, A+B=111...
2진 보수(TWO’S COMPLEMENT): A+B=10, A+B=100, A+B=1000…
2진수의 1의 보수는 자신의 수를 반대(1<->0)으로 바꾸면 되고, 2의 보수는 1의 보수에 +1또는 주어진 수의 우단으로부터
최초의 유효 BIT까지는 그대로 두고 나머지를 모두 반대(1<->0)으로 바꾸면 된다.
- 정수 표현
정수형(고정 소수점, FIXED POINT NUMBER) 표현
1. 부호화 절대치(SIGNEAGNITUDE)
sign bit: 0 - ‘+'
1 - ‘-‘
정수의 부호와 절대치를 따로 보관한다.(음수표현은 절대치가 같은 양수와 부호만 다르다. 음의 0과 양의 0이 공존)
표현범위(n bit 사용) : -(2^n-1 -1)~(2^n-1 -1)
2. COMPLEMENT
보수(Complement)를 사용하는 방법
R의 보수 R-1의 보수가 존재한다
양수의 표현은 절대값 표현 방식과 동일
표현 범위(n bit 사용)
1’S COMPLEMENT : -(2^n-1 -1)~(2^n-1 -1)
2’S COMPLEMENT : -(2^n-1)~(2^n-1 -1)
3. 10진수형 정수 표현
Unpacked decimal
zoned demical이라 하며 EBCDIC의 숫자 표현과 동일
1byte —> 10진수 한자만 표현(연산에는 사용될 수 없으나, 입출력 가능)
Packed decimal
1byte에 2자의 10진수를 표현(BCD code 이용)
마지막 4개의 비트로 부호를 표현(연산에 이용, 입출력 불가능)
- 실수 표현(부동 소수점, Floating-point)
과학적 표기의 지수(exponent)를 사용하여, 소수점의 위치를 이동시킬 수 있는 표현 방법
표현의 범위가 확대
비트 수에 따른 분류가 가능하다.
- 부호비트
- 지수(E)
- 기수(M)
ex) 32bit 체계의 겨우 부호비트1개 지수 8개 기수 23개의 비트 사용
0 0000 0101 1001 0000 0000 0000 0000 000
부호비트 0: 양수
지수(E) 000 0101: 5(usigned 8bit에 bias 127을 빼는 방식으로 표현)
기수(M) 1001 0000 0000 0000 0000 000
—
+ 0.1001x2^5

- 디지털 코드
BCD 코드(Binary Coded Decimal Code: 2진화 10진 코드, 8421 코드)
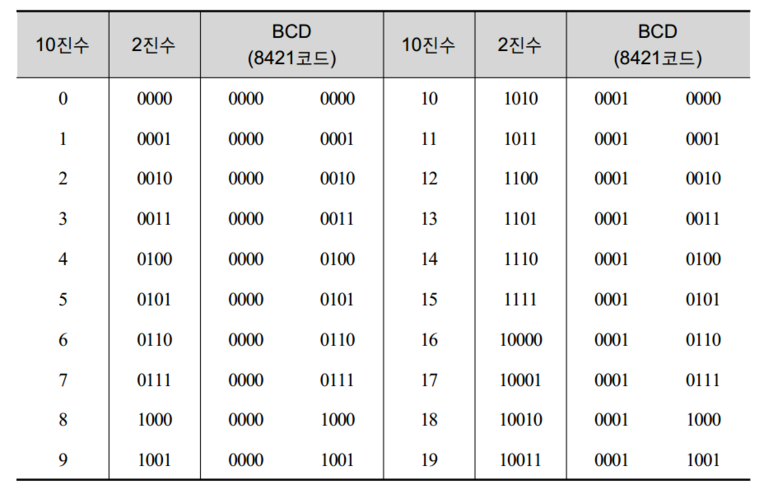
3초과 코드(excess-3코드)

1-9사이의 숫자들이 서로 보수 관계를 가지고 있다(ex 0-9, 1-8, 2-7 …)
초기에 통신에서 많이 사용됨
- 에러 검출 코드
패리티 비트

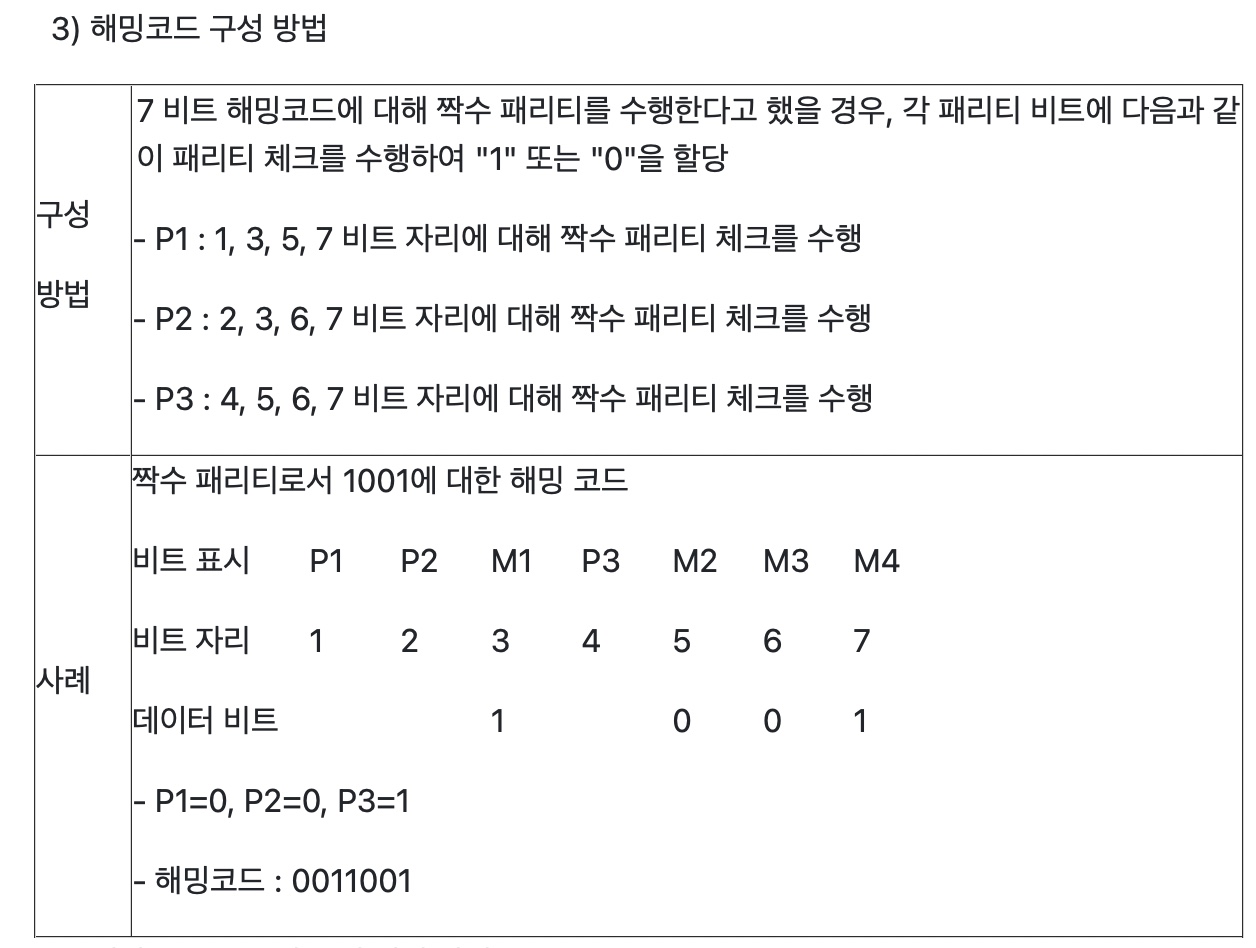
해밍 비트
8비트 데이터의 에러 정정 코드
정리
2진수-10진수
- 진 이진수
연산이 가능한 이진수
- 코드화 변환
- 정, 실수&연산용 변환(유효한 부분까지 이진화)
Complement
정해져 있는 범위 내에서 양수와 음수를 표현해야 하기 때문에
보수(Complement)를 사용해서 양/음수를 표현하기로 약속
2’s 보수에서는 음수 표현이 하나 더 많음(-127~126)
보수를 통해서 뺄셈의 연산을 덧셈으로 처리 가능
ex)10진 연산의 경우
32-12
32+87(12의 보수 87) 캐리연산은 0승자리에 더해줌